Scan
Conversion
Scan Conversion merupakan
metoda untuk memetakan titik ke dalam suatu pixel. Scan Conversion dapat
dilakukan terhadap Line (garis), polygon, ataupun garis lengkung (kurva).
Bicara soal garis, garis merupakan bentuk dasar dari sebuah gambar. Sedangkan
garis terbuat dari bentuk primitif yaitu sebuah titik. Terdapat beberapa
algoritma pembuatan garis yang sudah umum digunakan. Algoritma tersebut terdiri
atas :
1. Algoritma DDA
(Digital Differential Analyzer) Merupakan
algoritma untuk menggambar garis yang sederhana. Algoritma garis ini menggunakan perhitungan dx maupun dy,
menggunakan rumus dy = m . dx.
Garis dibuat menggunakan dua endpoint, yaitu titik awal dan titik akhir. Setiap
koordinat titik yang membentuk garis diperoleh dari perhitungan, kemudian
dikonversikan menjadi nilai integer.
Langkah-langkah
membentuk garis menurut algoritma DDA adalah :
1. Tentukan
dua titik yang akan dihubungkan dalam pembentukan garis
2. Tentukan
titik awal yaitu dan titik akhir .
3. Hitung dx = x1- x0 dan dy = y1 – y0
4. Tentukan step =
max( |dx| , |dy| )
5. Hitung
penambahan koordinat pixel XInc = dx / step dan YInc = dy / step
6. Koordinat
selanjutnya (x+XInc, y+yInc)
7. Posisi
pada layar ditentukan dengan pembulatan nilai koordinat tersebut
8. Ulangi
nomor 6 dan 7 untuk menentukan posisi pixel berikutnya. sampai x=x1dan
y=y1.
2. Algoritma Garis Bressenham
Algoritma
Bresenham pada tahun 1965, melakukan perbaikan dari algoritma perhitungan
koordinat piksel. Prosedur untuk menggambar kembali garis dengan
membulatkan nilai x atau y ke bilangan integer memerlukan waktu. serta variabel
x,y maupun m memerlukan bilangan real karena kemiringan merupakan nilai
pecahan. Bressenham mengembangkan algoritma klasik yang lebih menarik, karena
hanya menggunakan perhitungan matematik dengan bantuan bilangan integer.
Dengan demikian tidak perlu membulatkan nilai posisi
pixel setiap waktu. Langkah-langkahnya adalah sebagai berikut :
1. Tentukan dua
titik yang akan dihubungkan dalam pembentukan garis.
2. Tentukan salah
satu titik disebelah kiri sebagai titik awal (x0,y0) dan
titik lainnya sebagai titik akhir (x1,y1)
3. Hitung dx,
dy, 2dx dan 2dy-2dx
4. Hitung parameter
P0 = 2dy – dx
5. Untuk setiap
xk sepanjang garis dimulai dengan k=0
- Bila Pk < 0 maka
titik selanjutnya adalah (xk+1, yk) dan Pk+1=Pk+2dy
- Bila tidak maka titik selanjutnya
adalah (xk+1, yk+1) dan Pk+1=Pk+2dy-2dx
6. Ulangi nomor 5
untuk menentukan posisi pixel selanjutnya sampai x=x1 dan y=y1
Dalam
pembuatan garis, ada beberapa hal yang harus diperhatikan, hal tersebut ialah :
-
Ketebalan garis (thickness) dan
-
Bentuk tepi garis (ends).
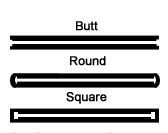
Bentuk
tepi garis ini dibagi menjadi 3, yaitu butt, round, square. Bentuk tepi garis butt akan memberikan garis sampai akhir
(berhenti garis tepat di akhir), tanpa ekstensi baris. Bentuk
tepi garis round adalah
default yang sering digunakan. Bentuk tepi garis square akan memberikan ujung persegi,
dengan perpanjangan garis.
Contoh dari bentuk tepi garis tersebut dapat di lihat di gambar
bawah ini.
Selain tepi garis, garis juga dapat digabungkan. Penggabungan garis (joining) terbagi menjadi :
-
Mitter
>> titik pertemuan 2 garis lurus yang membentuk
sudut lancip.
-
Round
>> titik sudut pertemuan yang membulat.
-
Bevel
>> titik sudut pertemuannya tampak terpotong rata.
-
None
>> titik sudut pertemuan yang terpotong agak
membentuk siku.
TRANSFORMATIONS
Transformation adalah suatu metoda untuk
mengubah lokasi titik. Operasi-Operasi Primitive pada Transformations terbagi
menjadi:
Ø Scale
Ø Rotate
Ø Shear
Ø Flip
Ø Translate
Contoh
gambar suatu objek :
Hasil dari transformasi gambar objek diatas :
a. Scale adalah skala pengali sama untuk semua komponen
b. Rotate/Rotasi adalah merotasi atau memutar suatu objek dengan nilai yang ditentukan. Dibawah ini adalah Rotasi terhadap titik (0,0) sebanyak 450 .
c. shear terhadap sumbu y
d. Flip terhadap sumbu x
e. Translate. (tx,ty) disebut vector Translasi
Perbedaan
antara Linear Transformation dan Non-Linear Transformation adalah model linier menunjukkan hubungan antara dua variable mengikuti garis lurus. Sedangkan non linier
mengikuti garis
yang tidak lurus,
misalnya kuadratik
(garisnya melengkung keatas lalu turun kebawah).
contoh Linear
Transformation dan Non-Linear Transformation dari Operasi-Operasi Primitive
transformation :
Ø Linear transformation
Ø Non-linear transformation
Perbedaan
antara Geometric Transformation dan Color Space Transformation adalah sebagai berikut :
Ø
Transformasi Geometrik
adalah transformasi berdasarkan perpindahan geometrik suatu titik Transformasi
ini terdiri dari translasi, skala dan rotasi, sedangkan
Ø
Color Space Transformation
membahas cara-cara mentransfomasi warna dalam model warna tertentu saja
dilakukan dengan cara Formulasi, Komplemen warna, Pemotongan warna, Koreksi
warna, Pemrosesan histogram.
Koordinat Homogen
(Homogeneous Coordiantes) adalah Koordinat homogen
adalah representasi koordinat 2 dimensi dengan 3 vektor. Setiap
koordinat posisi (x,y) direpresentasikan dalam bentuk koordinat homogen (xh,yh,h);
Paling sederhana: h = 1 à
(x,y,1) .
PROYEKSI
Proyeksi merupakan salah satu jenis transformasi, yaitu transformasi
koordinat. Proyeksi pada bidang datar (planar) dilakukan melalui sinar proyeksi
yang muncul dari titik pusat proyeksi melewati setiap titik dari benda dan
memotong bidang proyeksi (projection plane) untuk mendapatkan benda hasil
proyeksi. Proyeksi Planar (Planar Geometric Projections) dibedakan menjadi:
1.
Proyeksi Paralel.
Berdasarkan hubungan antara
arah proyeksi dengan vektor normal dari bidang proyeksi, proyeksi paralel
dibedakan menjadi:
a.
Orthographic
Proyeksi
Orthographic diperoleh
apabila sinar proyeksi tegak lurus dengan bidang proyeksi. Proyeksi orthographic sering
digunakan untuk menghasilkan tampak depan, tampak belakang, tampak samping dan
tampak atas dari sebuah benda atau disebut sebagai Multiview orthographic.
Tampak
atas, tampak belakang dan tampak dari samping sebuah benda sering disebut
sebagai elevation. Sedangkan
tampak dari atas disebut sebagai plan
view.
Transformasi untuk proyeksi multiview orthographic dapat
diperoleh dengan rumus :
Proyeksi
terhadap bidang x-z:qx = px,qy =pz
Proyeksi
terhadap bidang y-z:qx = px,qy =pz
Proyeksi
terhadap bidang x-y:qx = px,qy =py
Proyeksi orthographic ada yang disebut proyeksi axonometric. Proyeksi Axonometric dibedakan menjadi proyeksi:
Ø isometric,
Ø dimetric, dan
Ø trimetric.
a.
Oblique.
Proyeksi oblique diperoleh dengan cara membuat
sinar proyeksi tidak tegak lurus terhadap bidang proyeksi.
1.
Proyeksi Perspektif.
Memberikan
sudut pandang yang lebih realistis dibandingkan proyeksi orthographic. Proyeksi
perspektif pada kenyataannya jarak benda terhadap kita akan mempengaruhi
bagaimana benda tersebut terlihat. Benda yang terlihat jauh akan kelihatan
kecil sedangkan benda yang dekat akan terlihat lebih besar. Efek ini disebut
sebagai shortening. Pada perspektif semua garis menghilang pada satu atau lebih
titik yang sama atau disebut titik hilang (vanishing point).
Contoh dari proyeksi perspektif :
Perbedaan antara proyeksi parallel &
perspektif secara umum ialah pada proyeksi parallel jarak antara titik pusat
proyeksi ke bidang proyeksi tidak terhingga, sementara para proyeksi perspektif
jarak antara titik pusat proyeksi ke bidang proyeksi bersifat infinite
(tertentu).
Untuk mengetahui perbedaan lain antara kedua
proyeksi tersebut, dapat dilihat pada tabel perbandingan di bawah ini.
REFERENSI :
elib.unikom.ac.id
thesis.binus.ac.id
http://www.scribd.com/doc/21377284/Bab-VII-Transformasi-Linear
rekan kerja :
























0 komentar:
Posting Komentar